2. Формы представления гравитационного поля Земли.

2.1. Притяжение объемного тела.

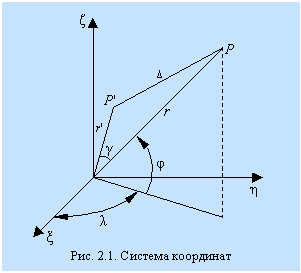Рассмотрим задачу о притяжении материальной точки P единичной массы телом М, следуя (Аксенов, 1977; Аксенов, 1986). Будем предполагать, что тело имеет произвольную форму, а плотность распределения масс является кусочно-непрерывной функцией координат.

Выберем прямоугольную, жестко связанную с телом систему координат Оxhz с началом в центре масс тела.

Пусть элемент объема dt тела М находится в точке P¢(x¢,h¢,z¢), плотность распределения масс обозначим через . Тогда потенциал притяжения или силовая функция тела М в точке P(x,h,z) определяется формулой

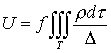, (2.1)

где f — постоянная тяготения, — расстояние точки P(x,h,z) от текущей точки P¢(x¢,h¢,z¢), T-объем, занятый телом М.

Если обозначить через r и r′ радиус-векторы точек P и P' , через — угол между ними, то ∆ и γ можно записать в виде:, где .

Потенциал U обладает, как известно (Дубошин, 1968), следующими свойствами.

1. Потенциал U есть функция, непрерывная во всем пространстве, обращающаяся в нуль в бесконечности, причем , где m—масса тела.

2. Частные производные первого порядка от потенциала U по координатам являются непрерывными функциями во всем пространстве и обращаются в нуль в бесконечности.

3. Если через X,Y,Z обозначить проекции силы притяжения точки P телом M на координатные оси Oξ, Oη, Oζ, то во всем пространстве

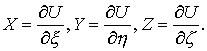
4. Во внешнем относительно тела M пространстве потенциал U удовлетворяет уравнению Лапласа:

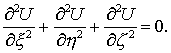
5. Внутри тела M потенциал U удовлетворяет уравнению Пуассона:

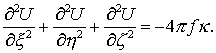
Для доказательства первых 4-х свойств достаточно, чтобы функция θ была кусочно-непрерывной, а для доказательства условия 5 требуется выполнение условия Гольдера, которое состоит в том, что для точки P, лежащей внутри тела M, всегда найдется объем dτ, содержащий точку P, что для любых двух точек (ξ₁,η₁,ζ₁) и (ξ₂,η₂,ζ₂) этого объема имеет место неравенство:

,

где — расстояние между точками, А и α—постоянные величины, причем 0<α<1.

Это условие будет выполнено, если плотность имеет непрерывные частные производные первого порядка. Эти свойства полностью определяют потенциал притяжения точки M и могут быть использованы для его практического определения. Возможен, конечно, и другой подход, который заключается в непосредственном вычислении интеграла (2.1). Однако, в конечном виде этот интеграл берется только в некоторых частных случаях: однородный шар, шар с концентрическим распределением плотности, однородный двухосный или трехосный эллипсоид.

Как известно, для концентрического шара потенциал дается формулой

.

В общем случае, рассмотренном в начале этого раздела, интеграл (2.1) можно вычислить только при помощи ряда. Наибольшее распространение получило в настоящее время разложение потенциала в ряд по сферическим функциям.

2.2. Основные сведения о полиномах Лежандра.

Остановимся на основных свойствах полиномов Лежандра

Полином Лежандра P_n(z) порядка n можно определить формулой Родрига:

(2.2)

Выпишем несколько первых P_n(z):

,

, (2.3)

,

,

и т.д.

Формулу (2.2) можно преобразовать к виду

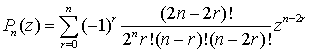, (2.4)

где , или , смотря по тому, какое из этих чисел целое.

Полиномы Лежандра высших порядков могут быть вычислены при помощи рекуррентного соотношения

. (2.5)

Кроме того, существуют формулы:

(2.6)

. (2.7)

Свойства полиномов Лежандра:

1. Полином Лежандра является четной или нечетной функцией в зависимости от того четна или нечетна его степень, так что .

2. На границах интервала [-1,1] полином Лежандра принимает следующие значения:

,.

3. Для любого z из промежутка (-1,1), при n>0

.

4. При больших n справедлива оценка

.

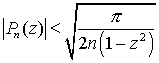5. Справедлива формула Лапласа

.

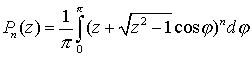6. Производящей функцией для P_n(z) является функция , так что

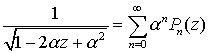. (2.8)

7. Полином Лежандра удовлетворяет следующему дифференциальному уравнению второго порядка

,

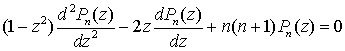называется уравнением Лежандра.

2.3. Присоединенные функции Лежандра. Общее выражение для сферических функций.

Присоединенную функцию Лежандра P_n,m(z) порядка n и степени m можно определить формулой:

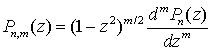, (2.9)

где P_n(z) — полином Лежандра.

Используя формулы (2.3), можно получить

,

,

,

,

и т.д.

Для вычисления можно использовать следующие рекуррентные соотношения:

, (2.10)

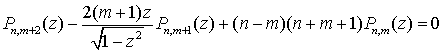. (2.11)

При этом достаточно пользоваться первой формулой, принимая во внимание, что, .

Присоединенные функции Лежандра являются составными элементами сферических функций. Функции двух аргументов P_n,m(cosθ)cosmψ, P_n,m(cosθ)sinmψ называются элементарными сферическими функциями.

Сферическая функция порядка n определяется формулой

,

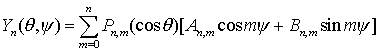где A_n,m, B_n,m произвольные постоянные.

Функция Y_n удовлетворяет следующему уравнению в частных производных

,

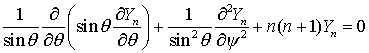а присоединенная функция Лежандра P_n,m является одним из решений уравнения

,

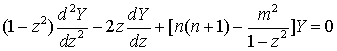которое при m=0 переходят в уравнение Лежандра.

Приведем формулу, которая носит название теоремы сложения для полиномов Лежандра:

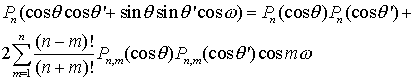. (2.12)

И еще одно свойство: интеграл по поверхности сферы единичного радиуса от произведения элементарных сферических функций различных порядков и степеней равных нулю. В то же время

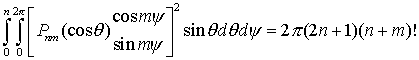. (2.13)

2.4. Нормированные и полностью нормированные функции Лежандра.

В динамике ИСЗ используются как присоединенные функции, так и нормированные и полностью нормированные функции Лежандра. Пусть P_т,m дается равенствами (2.9) и (2.4)

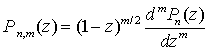, а 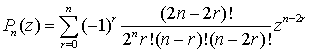(2.14)

Тогда нормированная присоединенная функция Лежандра P^'_nm задается формулой

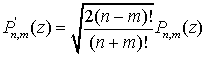, (2.15)

а полностью нормированная функция — формулой

,

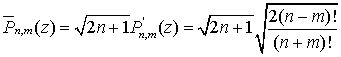
и таким образом, учитывая (2.14)

,

,

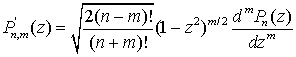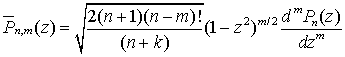где P_n(z) полином Лежандра.

Используемое здесь нормирование имеет следующий смысл:

Для P_nm согласно (2.13) имеем

,

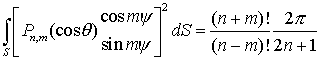а для и будем иметь:

,

,

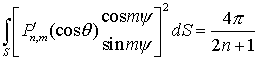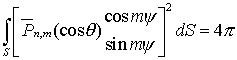где S—поверхность сферы единичного радиуса.

2.5. Разложение потенциала в ряд по сферическим функциям.

Как и ранее будем предполагать, что притягивающее тело имеет произвольную форму, а плотность является кусочно-непрерывной функцией координат. Тогда в системе координат Оξηζ, жестко связанной с телом, потенциал U в точке P(ξ,η,ζ) согласно (2.1) задается формулой:

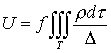, (2.16)

где f—постоянная тяготения,, , причем r—радиус-вектор точки P, а r',ξ',η',ζ'—радиус-вектор и координаты точки , в котором находится элемент объема dτ. Предположим, что точка P лежит вне притягивающего тела. Разложим в ряд 1/Δ. Для этого представим 1/Δ в виде:

.

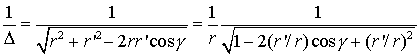Это дает возможность применить формулу (2.8), полагая α=r^'/r. Получаем

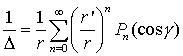(2.17)

и подставляя эту формулу в (2.16) будем иметь

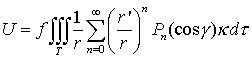. (2.18)

Перейдем к полярным (или сферическим) координатам:

, , ,

, , .

Тогда cosγ можно записать в виде:

.

Для того чтобы представить правую часть (2.18) в полярных координатах, воспользуемся теоремой сложения для полиномов Лежандра (2.12).Это дает

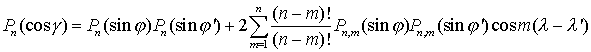. (2.19)

Далее, поскольку

равенство (2.19) примет вид

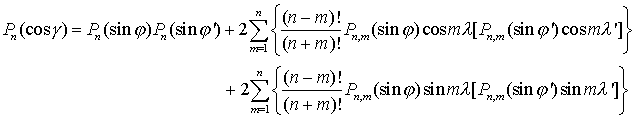
Если теперь представить эту формулу в (2.18) и ввести обозначения

,

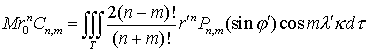, (2.20)

,

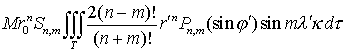где M—масса тела, r₀—некоторая линейная величина для земного экваториального радиуса. Величины J_n, C_n,m, S_n,m являются безразмерными. С учетом сказанного, мы получаем хорошо известные разложения потенциала U:

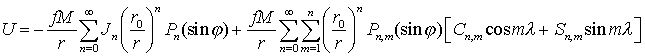. (2.21)

Коэффициенты J_n, C_n,m, S_n,m зависят от формы тела и распределения массы внутри него. Рассмотрим первые из них. Пусть в (2.20) n=0. Т.к.

, а ,

то

(2.22)

Далее, положим в (2.20) n=1, m=1,

,

и

и аналогично

,

ξ₀, η₀, ζ₀—координаты центра масс тела. Поскольку система Oξηζ находится в центре масс

, , (2.23)

Для n=2, m=1, m=2 можно получить

, , ,

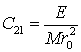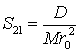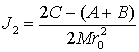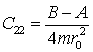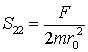, , (2.24)

где A, B, C– главные центральные моменты инерции, D, E, F – произведения инерции, т.е.

,

,

,

,

,

.

Учитывая перечисленные свойства U можно переписать в виде

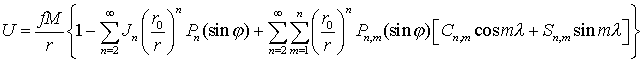. (2.25)

Замечания:

1. Разложение потенциала U сходится абсолютно и равномерно при , где r—расстояние для наиболее удаленной т. поверхности тела от его центра.

2. Если одна из осей, скажем , совпадает с главной центральной осью инерции, тогда D=0, E=0, а следовательно C₂₁=0, S₂₁=0. Если все три координаты совпадают с главными центральными осями инерции, тогда и коэффициент S₂₂=0.

3. Если плотность κ является функцией времени, то и коэффициенты , , являются функциями времени, а если κ постоянна, коэффициенты также постоянны.

2.6. Различные формы записи потенциала притяжения Земли.

1. Стандартная, утвержденная комиссией №7 МАС

.

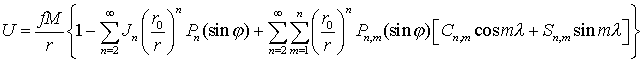2. Формула, применяемая в теоретических расчетах

,

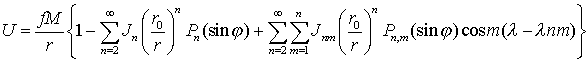где связь с коэффициентами C_n,m, S_n,m задается формулами:

, , , .

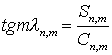3. Нормированная формула .

,

.

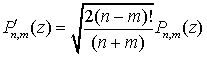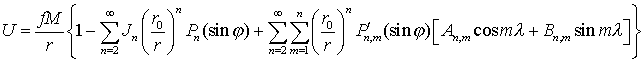4. Полностью нормированная функциями Лежандра

,

,

, .

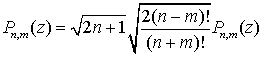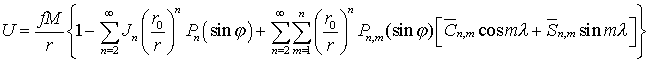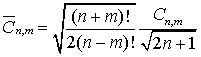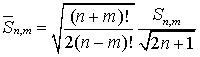5. Наиболее общая форма записи, используемая при численном моделировании

,

, , .

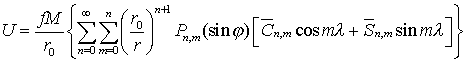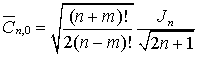В современных стандартных землях коэффициенты J_n не выделяются.

2.7. Структура разложения потенциала Земли.

Пусть

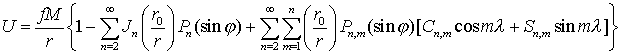. (2.26)

Все члены этого разложения можно разделить на три группы

1.Зональные гармоники. Пусть m=0, тогда имеем члены вида

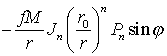. (2.27)

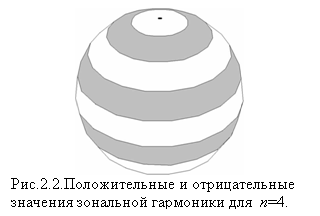Поскольку полином Лежандра P_n имеет n действительных различных корней по абсолютной величине меньших единицы, функция P_n(sinφ) на сфере будем менять знак на n параллелях, таким образом сфера разделится на n+1 широтную зону, в которой (2.27) будет принимать попеременно положительные и отрицательные значения. Этот член называется зональной гармоникой порядка n. На рис. 2.2 показано распределение положительных и отрицательных зон (показано для n=4).

2. Тессеральные гармоники. Пусть 0<m<n имеет члены

,

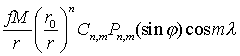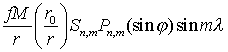, (2.28)

которые обращаются в нуль на n-m параллелях, определяемых уравнением

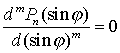
и 2m меридианах , .

3. Секторальные гармоники. Пусть, наконец, m=n, имеем члены

,

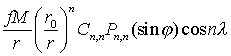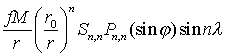(2.29)

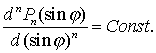
В этом случае, поскольку порядок дифференцирования и порядок полинома совпадают, формулы (2.29) обращаются в нуль только на меридианах, когда или .

Рассмотрим механический смысл различных слагаемых в (2.26). Самый первый член U представляет собой потенциал шара со сферическим распределением плотности, а все остальные члены характеризуют отличие Земли от тела сферической формы.

Вторая зональная гармоника характеризует полярное сжатие Земли и является основной характеристикой. Остальные дают более мелкие детали. Тессеральные и секторальные гармоники характеризуют отклонение Земли от тела динамически симметричного относительно оси вращения. Зональные гармоники, для которых n нечетно и тессеральные гармоники, для которых (n-m) нечетно определяют асимметрию Земли относительно экватора.

2.8. Определение постоянных гравитационного поля Земли. Стандартные Земли.

Числовые коэффициенты C_n,m и S_n,m разложения (2.26) потенциала Земли определяются как путем геодезических и гравиметрических измерений, так и с помощью наблюдений искусственных спутников Земли. Создание и уточнение гравитационных моделей Земли является одной из основных задач, которая решается с помощью наблюдений ИСЗ с одновременным привлечением геодезических и гравиметрических данных. В настоящее время в Смитсонианской астрофизической обсерватории получены модели гравитационного поля Земли под названием Стандартная Земля. Модель Стандартная Земля I получена на основе фотографических наблюдений спутников камерами Бейкера—Нанна. Стандартная Земля II включает в себя все коэффициенты разложения земного потенциала до шестнадцатого порядка включительно и некоторые гармоники более высокого порядка. Одновременно определялись координаты наблюдательной станции, причем точность определения координат многих станций 10 м и лучше.

Стандартная Земля III содержит зональные гармоники до 36 порядка, все тессеральные гармоники до 18 порядка и степени и некоторые гармоники более высоких порядков.

Годдардовский центр космических полетов, используя спутниковые и гравиметрические данные, получил более точные модели Земли—GEM (Goddard Earth Model). В настоящее время получены модели GEM9 и GEM10, причем GEM9 основана на оптических, лазерных и радиотехнических наблюдениях почти 30 спутников. Всего было использовано 840000 спутниковых измерений, из них почти 200000 лазерных наблюдений. МодельGEM10 объединяет спутниковые данные GEM9 с гравиметрическими измерениями. Использовались данные 1654 средних гравитационных аномалий на пятиградусных площадках, из них 1507 основывается на одноградусных аномалиях, в то время как остальные 147 были получены интерполяцией на пятиградусные площадки. При построении моделей GEM9 и GEM10 в отличие от более ранних моделей определялись дополнительно три фундаментальных геодезических параметра – средний радиус Земли r₀, гравитационная константа fm и среднее ускорение силы тяжести на экваторе g_e.

Современные модели гравитационного поля развиты до более высоких порядков и степеней. Так например, доступная через Интернет модель (JGM3) имеет порядок и степень, равные 360.

2.9. Представление потенциала Земли системой точечных масс

Другой способ представления потенциала Земли основан на использовании системы точечных масс. В этом случае потенциал U задается, как правило, формулой

. (2.30)

Здесь – потенциал задачи двух неподвижных центров (см. Раздел 5), а представляет собой потенциал точечной массы ,

,

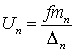где – расстояние до точечной массы с координатами .

Некоторые способы оптимального выбора параметров системы точечных масс можно найти в учебном пособии (Холшевников и др., 2005).

Далее