7. Численное моделирование движения ИСЗ

 

7.1. Особенности численного интегрирования уравнений движения ИСЗ

 

В иностранной литературе численные методы интегрирования называют еще методами частных (special) возмущений. Последняя терминология более ясно характеризует конечный результат рассматриваемых методов. Методы частных возмущений в отличие от аналитических (общих возмущений) вычисляют приращения к заданным значениям интегрируемых параметров, поведение которых задается дифференциальными уравнениями.  Поэтому численные методы интегрирования определяют частное решение дифференциальных уравнений, тогда как аналитические – общее.

Преимущество численных методов интегрирования состоит в том, что они не требуют упрощения правых частей дифференциальных уравнений, и позволяют учесть весь спектр действующих возмущений. В аналитических методах это практически неосуществимо.

Значительный недостаток методов частных возмущений связан с накоплением численной ошибки, обусловленной округлением. Очевидно, что  влияние ошибки округления можно ослабить за счет увеличения числа значащих разрядов. Этого можно достичь либо используя усовершенствованные вычислительные средства, либо преобразуя дифференциальные уравнений с использованием априорных сведений об их решении.

Ввиду того, что частные возмущения аппроксимируются отрезком степенного ряда по независимой переменной, для обеспечения требуемой точности шаг интегрирования в численных методах выбирается существенно меньшим, чем в аналитических. Таким образом, задача Коши разбивается на множество подзадач со своими частными решениями, которые последовательно определяются шаг за шагом.

Многошаговость численного процесса также приводит к серьезным трудностям при интегрировании. В большинстве численных методов шаг интегрирования выбирается в зависимости от величин старших членов аппроксимирующей суммы. В случае, если старшие члены становятся достаточно большими, как например вблизи сингулярных точек, шаг интегрирования уменьшается. На исследуемом интервале это приводит к дроблению (уплотнению) шага и, как следствие, к умножению неустранимой ошибки округления на шаге.

Ляпуновская неустойчивость решений уравнений небесной механики, и уравнений движения ИСЗ в том числе,  усиливает влияние ошибки аппроксимации метода на шаге интегрирования, что при длительных интервалах прогнозирования приводит к большому накоплению суммарной ошибки.

Перечисленные особенности процесса численного интегрирования уравнений движения ИСЗ побуждают нас искать такие формы представления уравнений движения, и организации  численного процесса, которые позволили бы устранить или, хотя бы ослабить негативное влияние указанных выше факторов.  Детально мы рассмотрим эти способы в двух последующих главах, а в этой главе остановимся на алгоритмах вычисления возмущающих ускорений в движении ИСЗ, используемых в численном моделировании.

 

7.2. Рекуррентные алгоритмы для вычисления  шаровых функций Vnm и их производных

 

Алгоритм, предложенный Л. Каннингемом

 

Как правило, моделирование возмущений в численном прогнозировании движения ИСЗ производится в прямоугольных координатах, независимо от формы записи уравнений движения.

Будем использовать потенциал Земли в виде представления:

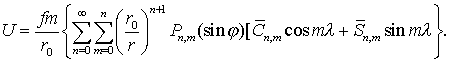                (7.1)

Введем шаровые функции , определяемые формулой

                            (7.2)

и представим (7.1) в виде

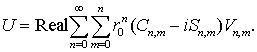                           (7.3)

Выразим x, y, z через :

Выразим  через x, y, z :

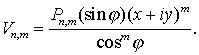                         (7.4)

Введем обозначени:

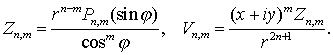  (7.5)

Можно записать явное выражение (Аксенов, 1986)

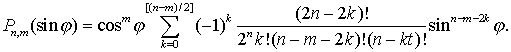   (7.6)

Используя (7.6) перепишем (7.5)

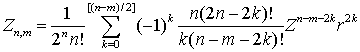
и введем функцию

                           (7.7)

которая является стандартной сферической гармоникой степени m порядка n.

Этот гармонический полином можно представить в операторной форме:

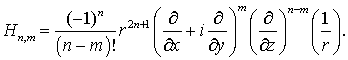                      (7.8)

Для m = n, учитывая (7.5), (7.7) и (7.8) можно записать

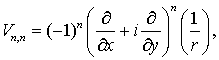                            (7.9)

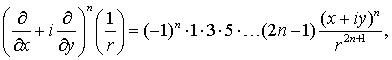
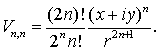                           (7.10)

Из (7.10) получается первое рекуррентное соотношение:

                       (7.11)

   Используем   рекуррентное соотношение (2.10) из главы 2 для присоединенных функций Лежандра

         (7.12)

для получения второго рекуррентного соотношения

                 (7.13)

Учитывая, что

Из (7.11) получим

Пусть n = m+1:

                                   (7.14)

Таким образом, начальные величины, необходимые для рекуррентного соотношения (7.13), задаются формулами (7.11) и (7.14), причем

следовательно

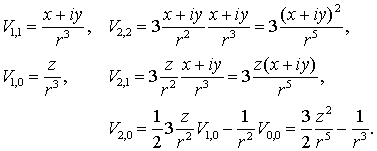
Выведем .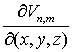

 Из (7.10)  получим

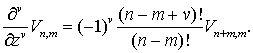                             (7.15)

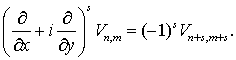
Это имеет место для неотрицательных значений n, m, s. Кроме того

 

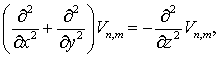
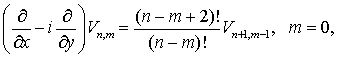                    (7.16)

Введем операторы

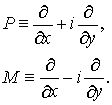
Очевидно, что

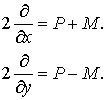
Используя выражения (7.15) и (7.16) и операторы P и M можно выписать необходимые рекуррентные соотношения:

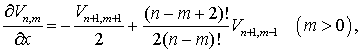
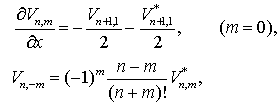
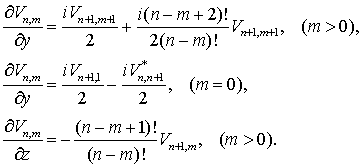                     (7.17)

Для полностью нормированных  функций Лежандра (см. раздел 2) эти соотношения будут иметь вид

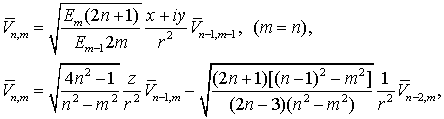
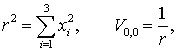
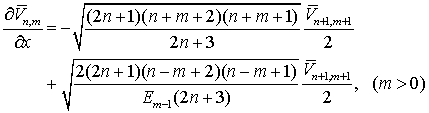
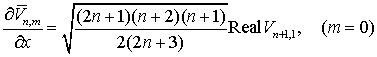
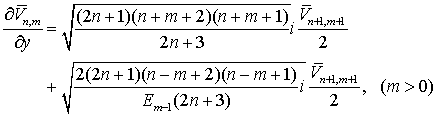                  (7.18)

 

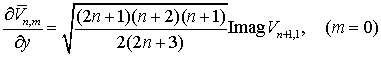
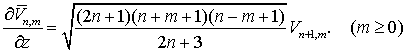
        Алгоритм, предложенный А. Дрожинером и В. Брумбергом.

 

Разделим  правую часть выражения (7.2)  на действительную и мнимую части

.                                             (7.19)

В результате этого выражение (7.1) для потенциала U   примет вид 

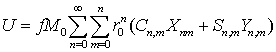.                       (7.20)

Выражение (7.20) можно получить и непосредственно из (7.1), вводя обозначения

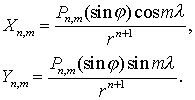                          (7.21)

Очевидно, что

                              (7.22)

Рекуррентное соотношение (2.11) из главы 2  для присоединенных функций Лежандра

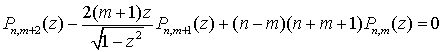
может быть использовано для получения первых рекуррентных соотношений для вычисления  функций. Действительно, используя (7.21) можно получить

,                            (7.23)

а в силу (7.22) будем иметь

                            (7.24)

Рекуррентное соотношение (7.12) для присоединенных функций Лежандра, позволяет получить два других рекуррентных соотношения

               (7.25)

и в силу (7.22)

                (7.26)

причем

         

        Что же касается формул для вычисления производных от функций , то их можно представить двумя способами. Либо получить  рекуррентные соотношения типа (7.25),(7,26), выражающие производные для  более высоких индексов n и m через производные для более низких индексов n и m, как это делает А. Дрожинер (Drozyner, 1977). Либо, как это предлагает В. Брумберг (1980), выразить производные через сами дифференцируемые функции. Остановимся на последнем подходе.

Аналогично (7.8) можно записать для  

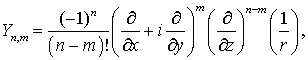                         (7.27)

что дает

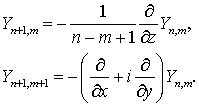                          (7.28)

В силу уравнения Лапласа

.

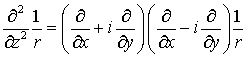Поэтому

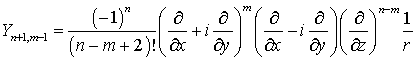
или

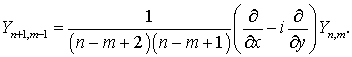                            (7.29)

Разрешая соотношения (7.27) – (7.29) относительно производных, получим

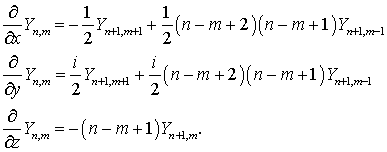         (7.30)

И далее использую соотношение (7.22) найдем

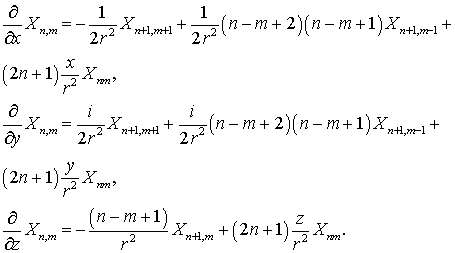             (7.31)

 

При m=0  формулы (7.30) и (7.31) значительно упрощаются.

        От действий с мнимыми величинами можно избавиться, если разделить функции  на мнимую и действительную части как это делается в (Брумберг,1980),  а можно использовать подход, предложенный К.В.Холшевниковым (Холшевников, 2005).

 

Алгоритм, предложенный К.В. Холшевниковым

 

        Будем использовать гравитационный потенциал в форме (7.20)

.

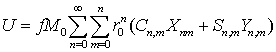        Как мы видели ранее, градиент шаровой функции сам является шаровой функцией, а ее порядок повышается на единицу, поэтому можно записать

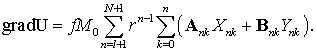  (7.32)

Остается только выразить  безразмерные компоненты  векторов  через , что можно сделать, используя рекуррентные соотношения.  Например, выражения для компонент  векторов , представленные  как линейные комбинации   , при ,   и при  будут иметь вид

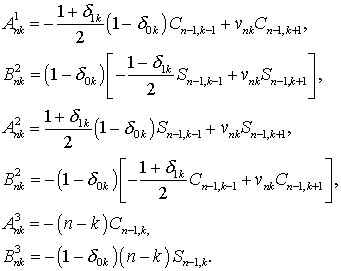
Здесь  – символ Кронекера,

Значения функций  в формуле (7.32) вычисляются по формулам (7.25) и (7.26).

 

7.3. Вычисление возмущений от приливных деформаций  центрального тела

 

В задачах численного моделирования движения ИСЗ все возмущения, связанные с Землей удобно вычислять с помощью рекуррентных соотношений, аналогичных описанным в предыдущем разделе. Обратимся вновь к формуле (4.2)

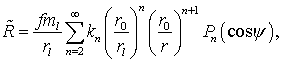                     (7.33)

где r – радиус-вектор внешней точки.

Поскольку Земля не является идеально упругим телом, приливной горб будет иметь некоторое запаздывание на угол  от направления на возмущающее тело, причем  может быть выражен через угол  и сферические координаты спутника  и возмущающего тела  следующим образом:

Воспользуемся известной теоремой сложения полиномов Лежандра, пронормируем полученные соотношения и, разделяя члены, относящиеся к сферическим координатам спутника и возмущающего тела, введем шаровые функции

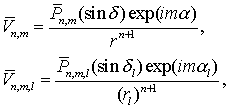                             (7.34)

и перепишем разложение (7.33) в виде

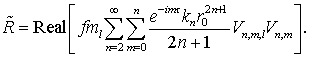                     (7.35)

Здесь  – нормированные  присоединенные функции Лежандра (см. раздел 2). Шаровые функции  и их производные по прямоугольным координатам могут вычисляться с помощью рекуррентного алгоритма Каннингема.

Сравнивая выражения (7.12) и (7.20), можно получить формулу для разложения геопотенциала, искаженного за счет приливной деформации.

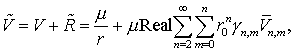
где  а  определено формулой

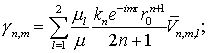
 причем l – номер возмущающего тела.

Для более точного учета влияния приливных деформаций можно использовать модель Вара. Различие между моделью Вара и Лява вводится в разложение V также в виде поправок [99] к нормализованным гармоническим коэффициентам:

                            (7.36)

 

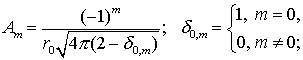
 ( – числа из модели Вара, k2 – номинальное число Лява); HS – амплитуда членов с индексом (табл. 2.1);

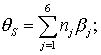                                      (7.37)

 – шестимерный вектор множителей к переменным Дудсона;  – переменные Дудсона, связанные с фундаментальными аргументами  (см. раздел 1) соотношениями:

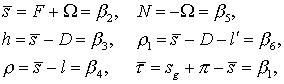
где  – среднее звездное время нулевого меридиана.

 

Таблица 7.1.

Коэффициенты для вычисления поправок к  и

за счет различия моделей Вара и Лява

Числа

Дудсона

h

N

Суточные эффекты (n = 2, m = 1)

145.555 (O1)

1

-1

0

0

0

0

-16.4

163.555 (P1)

1

1

-2

0

0

0

-49.6

165.545

1

1

0

0

-1

0

-9.4

165.555 (K1)

1

1

0

0

0

0

507.4

165.565

1

1

0

0

1

0

73.5

166.554

1

1

1

0

0

-1

-15.2

Полусуточные эффекты (n = 2, m = 2)

257.55 (M2)

2

0

0

0

0

0

39.5

273.555 (S2)

2

2

-2

0

0

0

18.4

 

        Более полные данные по вычислению поправок к коэффициентам  и  можно найти в (IERS1996).

Динамический эффект от океанических приливов учитывается в виде периодических вариаций нормализованных гармонических коэффициентов  . Вариации определяются формулой

             (7.38)

где

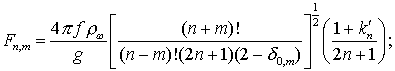
 f – универсальная гравитационная постоянная, равная   – плотность морской воды,  kn – нагрузочные деформационные коэффициенты (      – океанические приливные коэффициенты по m для приливной составляющей s (см. IERS96);  – аргумент приливной составляющей s, определенный формулой (7.22).

При вычислении суммы  выбор верхнего знака означает суммирование выражений, связанных с наступающими волнами  и , выбор нижнего знака выражений, связанных с отступающими волнами , . Океанические приливные коэффициенты, используемые здесь, связаны с амплитудами и фазами Свидерского формулой

где  – океанические приливные амплитуды для составляющей, обозначения Свидерского;  – океанические приливные фазы для s-й составляющей;

Таким образом, соотношения (7.38) могут быть записаны в одной из нижеследующих форм:

или

или

При суммировании по s(n,m) следует включать все составляющие, входящие в модель Свидерского (см IERS96), за исключением случаев, близких к резонансу, когда члены, связанные с отливом, не производят орбитальных возмущений долгого периода (>1 дня) для суточных и полусуточных приливов. Для спутников типа Лагеос, например, возмущения вдоль орбиты, связанные с комбинацией всех отступающих волн, меньше 5 см. Для долгопериодических приливов членами, связанными с отступающей волной, можно пренебречь, если удвоить члены, связанные с наступающей волной.

Для вычисления возмущений в наклонении и узле орбиты требуются только члены с четными степенями (n). При вычислении возмущений эксцентриситета и наклонения членами с нечетными степенями пренебрегать уже нельзя. Долгопериодические возмущения появляются только тогда, когда степень (n) больше, чем 1 (для суточных приливов), 2 (для полусуточных приливов). Наконец, амплитуды океанических приливов и их влияние на спутниковую орбиту убывают с возрастанием так, что для Лагеоса, например, достаточно ограничиться  n = 6.

Таким образом, для суточных приливов необходимо вычислять члены с n= 2, 3, 4, 5, 6 и m = 1; для полусуточных приливов  – только с и для долгопериодических приливов  – только с n = 2, 3, 4, 5, 6 и m = 0. В прил. 2 даны необходимые величины океанических приливных коэффициентов из модели Свидерского. Единицей измерения является 1 см. Для учета атмосферных приливов в качестве   и  нужно выбрать  

 

7.4. Особенности представления других возмущений в численном моделировании движения ИСЗ

 

Вычисление лунно-солнечных возмущений

 

Распространенным способом определения координат Луны является использование упрощенной теории Хилла-Брауна, координат Солнца – теории Ньюкома.

Следует, однако, иметь в виду, что при прогнозировании движения высоколетящих объектов этот способ задания координат Луны и Солнца вносит значительные ошибки в вычисленные положения спутника.

Ошибки прогнозирования можно существенно уменьшить, если использовать для вычисления координат Луны и Солнца в высокоточной теории движения этих объектов. В настоящее время известно две высокоточные теории движения больших планет, Солнца и Луны: американские DE200/LE200 и DE405/LE405, и французская VSOP82/LP2000.

Теории DE200/LE200 и DE405/LE405, полученные численными методами, охватывают период 1600-2200гг. и дают координаты в виде полиномов Чебышева в прямоугольной барицентрической системе координат с экватором Земли и равноденствием J2000.0. Теория VSOP82/LP2000 получена аналитически. Постоянные теории определялись из уравнения с численной теорией DE200/LE200. Координаты больших планет представлены в виде полиномов Чебышева на интервале времени 1735-2011 гг. В теории используются три системы координат: геоцентрическая, отнесенная к эпохе J2000.0 и две гелиоцентрические экваториальные, связанные с эпохами 1950.0 и 1975.0.

Можно отметить также, что применение аналитических теорий для вычисления координат Луны и Солнца в отличие от их табличного задания в машине делает алгоритмы численного прогнозирования движения ИСЗ автономными, не требующими предварительного вычисления таблиц, в тоже время табличный способ задания координат Луны и Солнца обладает большей оперативностью.

 

Вычисление возмущений от светового давления

 

 Как уже отмечалось в главе 4 основную трудность при вычислении возмущений, вызванных световым давлением, представляет учет эффекта вхождения спутника в тень Земли. С. Ферраз-Мелло предложил устранить эту трудность введением в возмущающее ускорение функции тени , причем , если спутник освещен Солнцем, , в противном случае. Рассмотрим случай, когда можно ограничиться цилиндрической формой тени и сформулируем условия вхождения спутника в тень.

Обозначим через - угол между осью цилиндра тени и вектором положения спутника. На промежутке  . Введем в рассмотрение угол , где -экваториальный  радиус Земли, .

Разобьем промежуток  на два:  и  и запишем функцию тени в виде

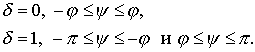                           (7.39)

Сила прямого светового давления с учетом тени перепишется следующим образом:

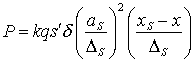.                            (7.40).

Аналитически условие вхождения в тень можно определит группой соотношений

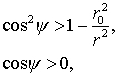                                  (7.41)

причем

.

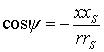Будем  далее считать, что тень Земли имеет форму кругового конуса (Бордовицына и др. 1992). В этом случае функция тени удовлетворяет следующим условиям:

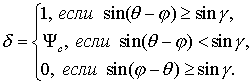                       (7.42)

Здесь

а значение теневой функции в области полутени  определяется в форме

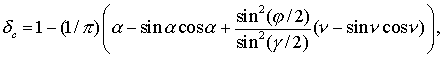        (7.43)

где – радиус Солнца,

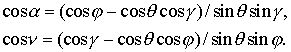
Сила, которая создается радиацией, отраженной от Земли, может быть представлена в форме

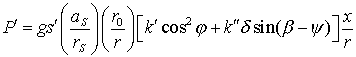.               (7.44)

Здесь через  обозначено такое значение угла , при котором диффузное отражение практически перестает оказывать влияние на спутник; — коэффициент инфракрасного отражения от Земли; — коэффициент радиального диффузного отражения. Значения коэффициентов  и  изменяются в пределах

, .

Функция  определена соотношениями

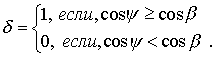                                   (7.45)

Значение угла подбирается экспериментальным путем.

 

Релятивистские эффекты

        Релятивистские поправки правых частей уравнений движения, записанных в геоцентрической системе координат, могут быть представлены согласно (Брумберг,199) в виде

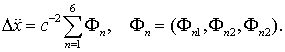                           (7.46)

Здесь – скорость света; – шварцшильдовские возмущения, определяемые полем тяготения Земли, рассматриваемой как сферически-симметричное тело; – эффекты лензе-терринговской прецессии, порожденной вращением Земли; – релятивистские квадрупольные члены; обусловленные наличием у Земли моментов инерции второго порядка; – релятивистские члены, обусловленные взаимодействием Земли и внешних масс (Луны–Л, Солнца–С), они описывают нелинейную суперпозицию гравитационных полей Земли и внешних масс; – релятивистские члены, которые можно интерпретировать как приливные возмущения от внешних масс; – поправки к ньютоновским возмущениям от внешних масс. Формулы для вычисления релятивистских ускорений  можно найти в (Brumberg, 2004).