8. Численные
методы высоких порядков для решения обыкновенных дифференциальных уравнений
(ОДУ)
8.1. Вводные
замечания
Современные
средства наблюдений позволяют получать пространственные положения ИСЗ с
точностью, равной 1 милиарксекунде. Как
показано в работе (Черницов, 2002), чтобы не потерять эту точность при
использовании наблюдений, нужно иметь возможность вычислять пространственные
положения ИСЗ с методической точностью, по крайней мере в три раза превышающей
точность наблюдений. Этого можно достичь только при применении в процессе моделирования движения ИСЗ численных методов
высоких порядков.
В данной
главе мы дадим описание наиболее часто употребляемых в практике моделирования
движения ИСЗ методов численного интегрирования обыкновенных дифференциальных
уравнений. К ним относятся явные одношаговые алгоритмы Рунге-Кутты-Фельберга (Fehkberg, 1969, 1972), высоких порядков, неявный одношаговый
алгоритм Эверхарта (Everhart, 1974а, 1974б), метод
рациональной экстраполяции Булирша и Штера (Bulirsh, Stoer, 1964,
1966; Stoer, 1974) и многошаговый алгоритм Адамса-Мультона-Коуэла
(Osterwinter, Cohen,1969)
Изложение
теории методов Рунге-Кутты можно найти в работах Дж. Батчера (Butcher, 1963, 1964), в двух написанных Дж. Батчером главах (5
и 10) книги «Современные численные методы решения обыкновенных дифференциальных
уравнений» (под редакцией Дж. Холла и Дж. Уатта (Холл и Уатт, 1979)),
опубликованной на русском языке в 1979 г., в монографии Т.В.Бордовицыной (1984)
и в книге Э. Хайрера, С.Нерсета и Г. Ваннера (1990). В приложении к последней
книге имеются также написанные на языке Фортран программы явных алгоритмов Рунге-Кутты (в модификации
Дормана и Принса) пятого и восьмого порядков для решения ОДУ первого и второго порядков.
Изложение метода Эверхарта, кроме указанных выше работ
самого автора, можно найти в монографии Т.В. Бордовицыной (1984).
Обоснование
экстраполяционных методов можно найти в монографии Дж. Штеттера (1978) и в
книге Э. Хайрера, С. Нерсета и Г. Ваннера (1990). В приложении к этой книге даны
программы (Фортран) экстраполяционных алгоритмов переменного шага и порядка для
решения ОДУ первого и второго порядка.
Изложение многошагового алгоритма Адамса-Мультона-Коуэла, кроме указанной
выше работы авторов можно найти в (Бордовицына, 1984).
8.2. Явные
одношаговые алгоритмы Рунге–Кутты–Фельберга
Явные
алгоритмы Рунге–Кутты, предложенные Э. Фельбергом, построены по типу вложенных
алгоритмов. Определение главного члена погрешности метода интегрирования на
одном шаге осуществляется в этих алгоритмах по двум формулам Рунге–Кутты смежных
порядков. Полученное значение главного члена ошибки метода на шаге используется
затем для выбора шага интегрирования, который основывается на требовании
одинаковой локальной точности вычислений на каждом шаге. Аналогичный же подход
к выбору шага можно найти в работе А. К. Платонова, З. П. Власовой и В. А. Степанянца
(Платонов и др., 1976).
Для
решения дифференциального уравнения
![]()
с начальным условием ![]() запишем две формулы
Рунге–Кутты смежных порядков:
запишем две формулы
Рунге–Кутты смежных порядков:
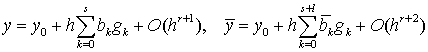 (8.1)
(8.1)
где
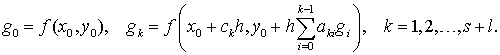 (8.2)
(8.2)
Для решения дифференциального уравнения
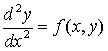
с начальными условиями ![]() будем использовать три
формулы:
будем использовать три
формулы:
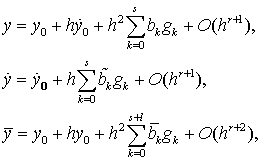 (8.3)
(8.3)
причем
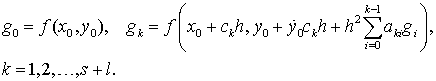 (8.4)
(8.4)
Здесь ![]() –
– ![]() –мерные векторы.
–мерные векторы.
Алгоритмы
Фельберга построены таким образом, что первые ![]() значений в формулах для
значений в формулах для
![]() и
и ![]() совпадают. Свободные
параметры среди
совпадают. Свободные
параметры среди ![]() выбираются из условия
минимума главной ошибки метода на шаге. Разность
выбираются из условия
минимума главной ошибки метода на шаге. Разность ![]() определяет величину
главного члена погрешности метода, имеющего порядок
определяет величину
главного члена погрешности метода, имеющего порядок ![]() , на одном шаге интегрирования. Контроль величины шага
интегрирования с помощью
, на одном шаге интегрирования. Контроль величины шага
интегрирования с помощью ![]() может быть осуществлен
следующим образом. Для всех интегрируемых уравнений на каждом шаге интегрирования
вычисляются величины
может быть осуществлен
следующим образом. Для всех интегрируемых уравнений на каждом шаге интегрирования
вычисляются величины
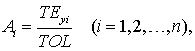 (8.5)
(8.5)
где ![]() – абсолютная точность
вычислений,
– абсолютная точность
вычислений, ![]() – относительная точность,
– относительная точность,
![]() – число интегрируемых
уравнений. Затем проверяется условие
– число интегрируемых
уравнений. Затем проверяется условие
![]()
где ![]() – порядок метода.
– порядок метода.
Если ![]() , новый шаг интегрирования уменьшается вдвое,
, новый шаг интегрирования уменьшается вдвое, ![]() , а если
, а если ![]() , то
, то ![]() . Этот критерий смены шага предложен Э. Фельбергом. Для определения
шага интегрирования может быть использована также формула Холла
. Этот критерий смены шага предложен Э. Фельбергом. Для определения
шага интегрирования может быть использована также формула Холла
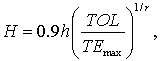
позволяющая непрерывно менять шаг интегрирования. ![]() есть максимальная величина
из всех
есть максимальная величина
из всех ![]() – константа,
подобранная эмпирически,
– константа,
подобранная эмпирически, ![]() – порядок метода.
– порядок метода.
Э.
Фельберг опубликовал алгоритмы 5 (6)–го и 7 (8)–го порядков для решения уравнений
первого порядка, получившие название алгоритмов Рунге–Кутты–Фельберга и полный
набор алгоритмов от 4 (5)–го и до 8 (9)–го порядков для решения уравнений второго
порядка без сведения их к уравнениям первого порядка. Эти алгоритмы названы
Фельбергом алгоритмами Рунге–Кутты–Нистрема (Fehlberg, 1972), так
как первые алгоритмы, предназначенные для непосредственного интегрирования
уравнений второго порядка, были даны А. Нистремом в 1925 г. Коэффициенты ![]() даны Э. Фельбергом в
виде рациональных дробей.
даны Э. Фельбергом в
виде рациональных дробей.
Возможность
производить оценку точности вычислений на каждом шаге с помощью главного члена
ошибки метода является большим достоинством алгоритмов Фельберга. Однако, как
отмечает Дж. Батчер, само вычисление главного члена ошибки метода в алгоритмах
Фельберга не для всех задач выполняется одинаково точно, поскольку практически
та и другая составные части метода основаны на одной и той же квадратурной
формуле.
Однако в
ряде задач небесной механики алгоритмы Фельберга оказываются достаточно гибкими
и дают хорошие результаты.
8.3. Неявный
одношаговый алгоритм Эверхарта
Рассмотрим основные принципы построения алгоритмов Эверхарта
на примере решения уравнений вида
![]() (8.6)
(8.6)
Пусть шаг интегрирования ![]() , начальное значения
, начальное значения ![]() в начальный момент
в начальный момент ![]() и
и ![]() – известные величины.
– известные величины.
Разложение
функции ![]() в ряд по степеням
в ряд по степеням ![]() в окрестности
в окрестности ![]() можно представить в
виде
можно представить в
виде
![]() (8.7)
(8.7)
Интегрируя уравнения () по независимой переменной,
получим
![]() (8.8)
(8.8)
Полином ![]() –ой степени, стоящий в правой части (8.7), не является отрезком
ряда Тейлора, поскольку коэффициенты
–ой степени, стоящий в правой части (8.7), не является отрезком
ряда Тейлора, поскольку коэффициенты ![]() вычисляются не по
известным формулам коэффициентов ряда Тейлора, а определяются из условий наилучшего
приближения
вычисляются не по
известным формулам коэффициентов ряда Тейлора, а определяются из условий наилучшего
приближения ![]() в момент времени
в момент времени ![]() конечными разложениями
(8.8).
конечными разложениями
(8.8).
Выразим
коэффициенты ![]() через разделенные
разности. Для этого представим функцию
через разделенные
разности. Для этого представим функцию ![]() в виде
в виде
![]() (8.9)
(8.9)
В каждый момент времени ![]() имеем
имеем
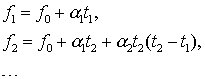 (8.10)
(8.10)
отсюда получим разделенные разности
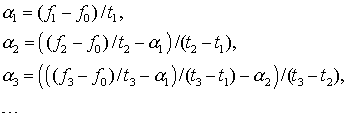 (8.11)
(8.11)
Приравнивая коэффициенты при одинаковых степенях ![]() , выразим коэффициенты
, выразим коэффициенты
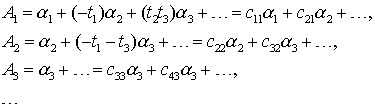 (8.12)
(8.12)
Для коэффициентов ![]() справедливы следующие
рекуррентные соотношения
справедливы следующие
рекуррентные соотношения
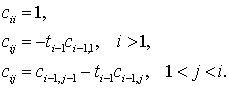 (8.13)
(8.13)
Таким
образом, нахождение решения уравнения (8.6) сводится, прежде всего, к нахождению
узлов разбиения ![]() шага
шага ![]() . Известно (Холл и Уатт, 1979), что за счет выбора разбиения можно
повысить порядок точности неявного одношагового метода с
. Известно (Холл и Уатт, 1979), что за счет выбора разбиения можно
повысить порядок точности неявного одношагового метода с ![]() до
до ![]() , если в качестве значений узлов разбиения
, если в качестве значений узлов разбиения ![]() , (
, (![]() ) выбрать корни полинома Лежандра
) выбрать корни полинома Лежандра ![]() степени
степени
![]()
Значения ![]() в моменты времени
в моменты времени ![]() определяются формулами
определяются формулами
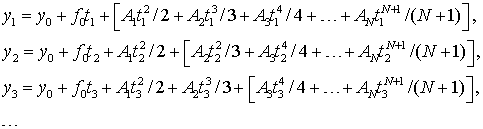 (8.14)
(8.14)
Эти предсказующие уравнения служат для определения
коэффициентов ![]() , а исправляющее уравнение
, а исправляющее уравнение
![]() (8.15)
(8.15)
дает значение решения на конце шага ![]() .
.
В
алгоритмах Эверхарта контроль шага интегрирования осуществляется по величине последнего
члена в разложении решения (8.15). Пусть ![]() есть контрольный параметр,
такой, что
есть контрольный параметр,
такой, что ![]() есть требуемая
точность вычислений. Введем величину
есть требуемая
точность вычислений. Введем величину ![]() , определяемую соотношением
, определяемую соотношением
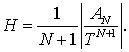
Новый шаг интегрирования ![]() определяется формулой
определяется формулой
![]()
Эффективность
процесса численного интегрирования во многом зависит от того, насколько удачно
осуществлен выбор начального шага. Для уравнений в нормализованном виде Э. Эверхартом
в качестве такого шага предложена некоторая величина, полученная путем экспериментальных
расчетов. Для метода интегрирования порядка ![]() она задается формулой
она задается формулой
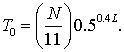
Оптимальное
значение параметра ![]() определяется опытным путем
в зависимости от типа интегрируемых дифференциальных уравнений. Если же
определяется опытным путем
в зависимости от типа интегрируемых дифференциальных уравнений. Если же ![]() слишком мало, шаг
может оказаться слишком большим и это ухудшит сходимость, а также точность метода.
Если же
слишком мало, шаг
может оказаться слишком большим и это ухудшит сходимость, а также точность метода.
Если же ![]() , наоборот, слишком велико, интегрирование будет выполняться точно,
но метод будет неэффективен по затратам машинного времени.
, наоборот, слишком велико, интегрирование будет выполняться точно,
но метод будет неэффективен по затратам машинного времени.
8.4. Экстраполяционные
алгоритмы
8.4.1. Экстраполяционные
схемы Невилла и Штера
Пусть ![]() есть дискретная
аппроксимация решения
есть дискретная
аппроксимация решения ![]() , определенная для шага
, определенная для шага ![]() , причем
, причем ![]() достаточно мало. В том
случае, если
достаточно мало. В том
случае, если ![]() имеет асимптотическое
разложение
имеет асимптотическое
разложение
![]() (8.16)
(8.16)
Л. Ричардсон (Richardson, 1910) предложил получать
улучшенную аппроксимацию из двух или более значений ![]() , определенных в
, определенных в ![]() , требуя, чтобы линейная комбинация
, требуя, чтобы линейная комбинация ![]()
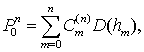 (8.17)
(8.17)
удовлетворяла условию
![]() (8.18)
(8.18)
в то время как ![]()
![]() .
.
Такую
процедуру построения улучшенной аппроксимации принято называть экстраполяцией,
поскольку она используется на каждом шаге интегрирования. Существенно, что
константы ![]() вычислять не нужно.
При экстраполяции полиномами
вычислять не нужно.
При экстраполяции полиномами ![]() может быть найдено непосредственно
по рекуррентному алгоритму Невилла, а при экстраполяции рациональными функциями
для этой цели может быть использован алгоритм Штера.
может быть найдено непосредственно
по рекуррентному алгоритму Невилла, а при экстраполяции рациональными функциями
для этой цели может быть использован алгоритм Штера.
Пусть ![]() есть полином степени
есть полином степени ![]() относительно
относительно ![]() , который интерполирует
, который интерполирует ![]() в точках
в точках ![]() . Тогда
. Тогда ![]() может быть найдено с
помощью следующей линейной рекуррентной схемы:
может быть найдено с
помощью следующей линейной рекуррентной схемы:
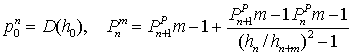 (8.19)
(8.19)
с диаграммой
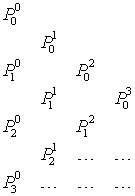 (8.20)
(8.20)
Как показано Ф. Бауэром, Х. Рутишаузером и Е. Штифелем
(Хайрер и др., 1990), эта последовательность преобразований сходится в ![]() . Основную вычислительную трудность составляет определение
первого столбца диаграммы
. Основную вычислительную трудность составляет определение
первого столбца диаграммы ![]() .
.
Пусть,
далее, ![]() есть рациональная
функция, числитель которой есть полином степени
есть рациональная
функция, числитель которой есть полином степени ![]() , а знаменатель – полином степени
, а знаменатель – полином степени ![]() . Функция
. Функция ![]() интерполирует
интерполирует ![]() в точках
в точках ![]() . Алгоритм Штера для последовательности
. Алгоритм Штера для последовательности ![]() дает следующую
рекурсивную схему построения функций
дает следующую
рекурсивную схему построения функций ![]() :
:
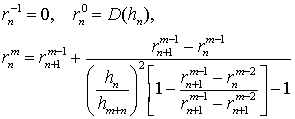 (8.21)
(8.21)
с диаграммой
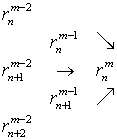 (8.22)
(8.22)
Исследование сходимости последовательности функций ![]() выполнено В. Греггом (Хайрер
и др., 1990).
выполнено В. Греггом (Хайрер
и др., 1990).
8.4.2. Метод
Булирша и Штера
Для того
чтобы применить локальную экстраполяцию к решению дифференциального уравнения
![]()
необходимо выбрать в качестве основы интегрирования
численный метод, для которого существует асимптотическое разложение вида (8.16).
В методе рациональной экстраполяции Булирша и Штера для этой цели используется
модифицированный метод прямоугольников:
![]()
![]()
Для ![]()
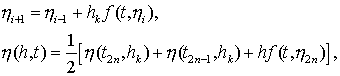 (8.23)
(8.23)
где ![]() а
а ![]() – основной шаг
интегрирования,
– основной шаг
интегрирования, ![]() – натуральное число,
– натуральное число, ![]() Тогда дискретная
аппроксимация решения
Тогда дискретная
аппроксимация решения ![]() определится следующим
образом:
определится следующим
образом:
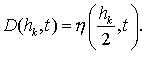 (8.24)
(8.24)
Авторы метода рекомендуют выбирать в качестве ![]() следующую последовательность
чисел:
следующую последовательность
чисел:
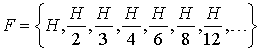 (8.25)
(8.25)
8.4.3. Выбор
шага интегрирования
Экстраполяционные
методы позволяют варьировать одновременно порядок метода, длину основного шага
интегрирования и количество этапов вычислений на каждом шаге. Одинаковой
точности вычислений можно добиться лишь увеличивая порядок метода, либо
увеличивая число этапов вычислений на шаге, либо уменьшая длину шага интегрирования.
Однако при практическом использовании метода следует учитывать, что влияние ошибки
округления растет с увеличением порядка экстраполяции. Поэтому во всех реализованных
на ЭВМ версиях алгоритма, начиная с первой программы Булирша и Штера (Bulirsch,
Stoer, 1966), порядок метода не превосходит шести. Авторами алгоритма предложено
два способа выбора шага интегрирования (Bulirsch, Stoer, 1966, Stoer, 1974).
Первый
способ, довольно грубый, но весьма простой и удобный для практической реализации,
состоит в следующем.
Пусть
необходимая точность вычислений достигается при порядке экстраполяции ![]() , т.е. при
, т.е. при ![]() и
и ![]() , выполняется неравенство
, выполняется неравенство
![]() (8.26)
(8.26)
где ![]() – заданная точность
вычислений,
– заданная точность
вычислений, ![]() , тогда длина основного шага интегрирования
, тогда длина основного шага интегрирования ![]() увеличивается и новый
шаг
увеличивается и новый
шаг ![]() вычисляется по формуле
вычисляется по формуле
![]() (8.27)
(8.27)
Если, напротив, требуемая точность не достигается
после девяти этапов, т.е.
![]() (8.28)
(8.28)
то шаг уменьшается и длина его определяется по формуле
![]() (8.29)
(8.29)
Во втором
способе выбора шага максимальный порядок экстраполяции не задается, а
вычисляется по формуле
![]() (8.30)
(8.30)
если ![]() , где символ
, где символ ![]() – означает целую часть
числа,
– означает целую часть
числа, ![]() – требуемое число значащих
цифр. Новый шаг
– требуемое число значащих
цифр. Новый шаг ![]() определяется формулой
определяется формулой
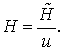 (8.31)
(8.31)
Корректирующий множитель ![]() задается группой
соотношений
задается группой
соотношений
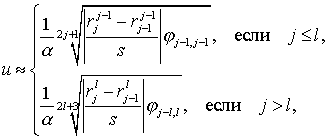 (8.32)
(8.32)
где
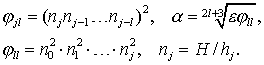
Далее, проверяется условие, является ли последний член
![]() достаточно точным,
т.е. имеет ли место соотношение
достаточно точным,
т.е. имеет ли место соотношение
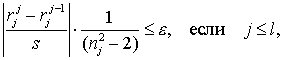
или
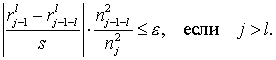
Если элемент ![]() достаточно точен,
решение полагается равным
достаточно точен,
решение полагается равным ![]() ,
, ![]() и новый шаг интегрирования
выбирается равным
и новый шаг интегрирования
выбирается равным ![]() . Если же элемент
. Если же элемент ![]() не является достаточно
точным и в то же время
не является достаточно
точным и в то же время ![]() . Если
. Если ![]() , вычисляется новый индекс
, вычисляется новый индекс ![]() , которым следует ограничить вычисление начального столбца таблицы
, которым следует ограничить вычисление начального столбца таблицы
![]() :
:
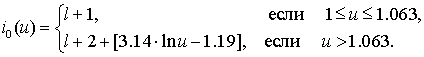 (8.33)
(8.33)
Если при этом количество перевычислений функций ![]() удовлетворяет соотношению
удовлетворяет соотношению
![]() (8.34)
(8.34)
то шаг уменьшается: ![]() . В противном случае индекс
. В противном случае индекс ![]() полагается равным
полагается равным ![]() и происходит простое
расширение таблицы
и происходит простое
расширение таблицы ![]() .
.
8.5. Многошаговые
методы
8.5.1.
Принципы построения
Линейные
многошаговые методы являются традиционным математическим аппаратом численного
решения уравнений движения небесных тел, как естественных, так и искусственных.
Более того, первые многошаговые методы были разработаны Адамсом и Коуэллом
для решения задач небесной механики.
Изложение многошаговых методов можно найти практически во всех учебниках,
касающихся численного решения обыкновенных дифференциальных уравнений (см.
например, Бахвалов, 1973), а также в некоторых учебниках и статьях по небесной
механике (Субботин, 1937; Чеботарев, 1965; Куликов, 1960; Oesterwintwer, Cohen, 1969)
Детальное изложение теории многошаговых методов можно найти в (Хайрер и др.,
1990). Поэтому в настоящем учебнике мы остановимся лишь на принципах построения
разностных формул и приведем получивший распространение в задачах небесной
механики алгоритм Адамса-Мультона-Коуэлла. Формулы для вычисления коэффициентов
этого метода были получены Ш. Коеном и Е. Хаббардом и приведены в работе (Oesterwintwer, Cohen, 1969) и
монографии (Бордовицына, 1984).
Одношаговые
методы, как мы видели ранее, для получения значения в y в
(n+1)-ой точке требуют
знания значение y в n-ой точке,
все же остальные значения для вычисления ![]() не используются. В многошаговых методах, наоборот, для
вычисления
не используются. В многошаговых методах, наоборот, для
вычисления ![]() используются некоторые
предварительно определенные значения
используются некоторые
предварительно определенные значения ![]()
Проинтегрируем
уравнение
![]() (8.35)
(8.35)
в пределах от t
до t+h и получим тождество
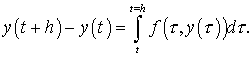 (8.36)
(8.36)
Заменим далее ![]() каким-либо интерполяционным полиномом
каким-либо интерполяционным полиномом ![]() принимающим значения
принимающим значения
![]() на множестве точек
на множестве точек ![]() для которых
для которых ![]() уже известны. Выбор
в качестве
уже известны. Выбор
в качестве ![]() интерполяционной формулы Ньютона с разностями назад определит
группу методов Адамса.
интерполяционной формулы Ньютона с разностями назад определит
группу методов Адамса.
При ![]() мы получим формулу метода Адамса-Башфорта в виде
мы получим формулу метода Адамса-Башфорта в виде
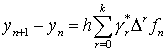 (8.37)
(8.37)
или в форме Лагранжа
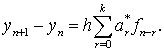 (8.38)
(8.38)
Причем ![]() - r-ая
разность функции f, а
- r-ая
разность функции f, а ![]() - значение функции в
точке
- значение функции в
точке ![]()
Полагая
![]() , будем иметь формулу
Адамса-Мультона в виде
, будем иметь формулу
Адамса-Мультона в виде
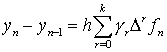 (8.39)
(8.39)
или в форме Лагранжа
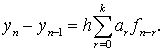 (8.40)
(8.40)
При выборе в
качестве ![]() интерполяционной формулы Стирлинга получим метод Коуэлла.
В существующем виде этот метод используется для решения уравнений второго порядка
без сведения их к уравнениям первого порядка и определяется формулой
интерполяционной формулы Стирлинга получим метод Коуэлла.
В существующем виде этот метод используется для решения уравнений второго порядка
без сведения их к уравнениям первого порядка и определяется формулой
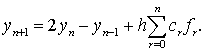 (8.41)
(8.41)
Общую формулу многошаговых методов можно принять
следующей:
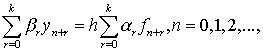 (8.42)
(8.42)
где ![]() - постоянные, причем
- постоянные, причем
![]() .
.
Если ![]() , многошаговый метод называется явным. Если же
, многошаговый метод называется явным. Если же ![]() , правая часть формулы
(8.42) содержит
, правая часть формулы
(8.42) содержит ![]() и формула представляет
собой нелинейное уравнение относительно
и формула представляет
собой нелинейное уравнение относительно![]() . В этом случае метод называется неявным многошаговым. Для
одних и тех же k неявный метод
является более точным, чем явный, поскольку обладает более высокой устойчивостью
к малым возмущениям
. В этом случае метод называется неявным многошаговым. Для
одних и тех же k неявный метод
является более точным, чем явный, поскольку обладает более высокой устойчивостью
к малым возмущениям ![]() . Поэтому на практике используются, как правило, неявные
многошаговые методы. Нелинейное уравнение (8.40) удобно переписать в виде
. Поэтому на практике используются, как правило, неявные
многошаговые методы. Нелинейное уравнение (8.40) удобно переписать в виде
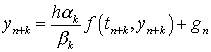 ,
, ![]() , (8.43)
, (8.43)
причем ![]() содержит известные величины
содержит известные величины ![]() . Существование и единственность
решения
. Существование и единственность
решения ![]() уравнения (8.41) для
известных многошаговых методов доказана П. Хенричи (Henrici, 1962).
уравнения (8.41) для
известных многошаговых методов доказана П. Хенричи (Henrici, 1962).
Коэффициенты
![]() для формул (8.37)-(8.40) до r =8
можно найти в книге (Хайрер и др., 1990). . Коэффициенты основных разностных
формул до 12 порядка можно найти в книге (Штифель, Шейфеле, 1975). Коэффициенты
методов Адамса-Мультона и Коуэлла до 16
порядка можно найти в работе(Oesterwintwer, Cohen, 1969) и
монографии (Бордовицына, 1984).
для формул (8.37)-(8.40) до r =8
можно найти в книге (Хайрер и др., 1990). . Коэффициенты основных разностных
формул до 12 порядка можно найти в книге (Штифель, Шейфеле, 1975). Коэффициенты
методов Адамса-Мультона и Коуэлла до 16
порядка можно найти в работе(Oesterwintwer, Cohen, 1969) и
монографии (Бордовицына, 1984).
Начальное
приближение определяется обычно с
помощью явной многошаговой формулы. В этом случае явный метод называется
предсказующим, а неявный метод исправляющим, а весь процесс отыскания решения ![]() называется методом
предсказания и коррекции. Для
применения многошаговой формулы на каждом k - м шаге интегрирования необходимо иметь так называемую
таблицу интегрирования, которая для
метода Адамса-Мультона состоит из величин
называется методом
предсказания и коррекции. Для
применения многошаговой формулы на каждом k - м шаге интегрирования необходимо иметь так называемую
таблицу интегрирования, которая для
метода Адамса-Мультона состоит из величин
![]() , (8.44)
, (8.44)
а для метода Коуэлла имеет вид
![]() , (8.45)
, (8.45)
где k – порядок аппроксимирующей формулы.
Вычисление
таблиц функций (8.44), (8.45) в начале интегрирования производится, как правило, с помощью какого-либо одношагового
метода, однако существуют и самостартующие многошаговые методы. К таким методам
относится самостартующий алгоритм метода Коуэлла, развитый Д.К. Куликовым
(1960).
Возможны два способа организации методов предсказания и коррекции. В первом способе итерации проводятся до тех пор, пока сходимость не будет достигнута.
При этом можно либо фиксировать шаг, оставляя число итерации произвольным, либо
фиксировать число итераций, оставляя произвольной величину шага. Такой метод
принято называть исправлением до сходимости. Поскольку в многошаговом методе
любое изменение шага приводит к перевычислению начальной таблицы интегрирования,
то с практической точки зрения гораздо более удобно фиксировать шаг, оставляя
число итерации произвольным.
Во втором
способе число применений исправляющей формулы фиксировано. Различные схемы
вычисления, которые в этом случае могут
быть использованы, в обозначениях Холла и Кримера записываются следующим образом
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Здесь P означает однократное применение предсказующей формулы,
C –
однократное применение исправляющей формулы, E – вычисление
функции f , m – число итераций.
8.5.2.
Алгоритм Адамса-Мультона-Коуэлла
Перейдем
к описанию метода Адамса-Мультона-Коуэлла, нашедшего широкое применение в
исследовании движения больших планет и
спутниковой геодезии. Метод предназначен для интегрирования
дифференциальных уравнений второго
порядка
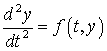 ,
, ![]() ,
, ![]() (8.46)
(8.46)
без сведения их к уравнениям первого порядка.
Для
построения метода используются формулы (8.40) и (8.41). Коэффициенты ![]() приведены в табл.8.1,
причем D – общий делитель, на который должны быть разделены
все числа в таблице.
приведены в табл.8.1,
причем D – общий делитель, на который должны быть разделены
все числа в таблице.
Таблица 8.1.
Коэффициенты методов Адамса и Коуэлла
|
j |
|
|
|
0 |
32011868528640000 |
32011868528640000 |
|
1 |
- 16005934246320000 |
- 32011868528640000 |
|
2 |
- 2667655710720000 |
2667655710720000 |
|
3 |
- 1333827855360000 |
0 |
|
4 |
- 844757641728000 |
- 133382785536000 |
|
5 |
- 600222534912000 |
- 133382785536000 |
|
6 |
- 456783110784000 |
- 116974585728000 |
|
7 |
- 363891528000000 |
- 100566385920000 |
|
8 |
- 299520219398400 |
- 86707632211200 |
|
9 |
- 252655401398400 |
-
75398324601600 |
|
10 |
- 217227737563200 |
- 66193573118400 |
|
11 |
- 189640115028000 |
- 58548487788800 |
|
12 |
- 167636336098320 |
- 52401453198480 |
|
13 |
- 149735464049160 |
- 47174128491600 |
|
14 |
- 134928496929540 |
- 42755108505900 |
|
15 |
- 122506205369730 |
- 38983584907800 |
|
16 |
- 111956703448001 |
- 35736323456205 |
|
D = 32011868528640000 |
||
Алгоритм
начинается вычислением вспомогательных
коэффициентов с использованием коэффициентов Адамса и Коуэлла, приведенных в
табл. 8.1. по формулам
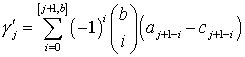 ,
, ![]() ,
,
где ![]() есть наименьшее их
есть наименьшее их![]() и
и ![]() ,
,
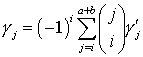 ,
, ![]() ,
,
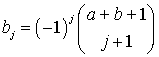 ,
, ![]() ,
,
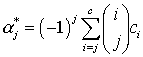 ,
, ![]() ,
,
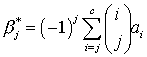 ,
, ![]() ,
,
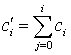 ,
, ![]() ,
,
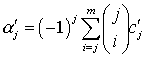 ,
, ![]() ,
,
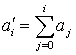 ,
, ![]() ,
,
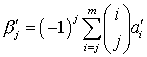 ,
, ![]() ,
,
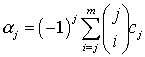 ,
, ![]() ,
,
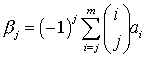 ,
, ![]() .
.
Здесь c и m порядки
начальной и основной аппроксимирующих формул метода соответственно, ![]() - биномиальные коэффициенты, параметры a
и b связаны с аппроксимирующей формулой, предназначенной
для вычисления величины
- биномиальные коэффициенты, параметры a
и b связаны с аппроксимирующей формулой, предназначенной
для вычисления величины
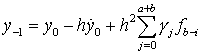 . (8.47)
. (8.47)
Неизвестные ускорения, входящие в формулу (8.47),
полагаются равными его начальному значению в интервале от a до b. Числа a и b не могут превосходить c. Вне интервала (a, b)
неизвестные ускорения вычисляются по формулам
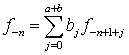 ,
, ![]()
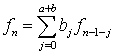
![]() (8.48)
(8.48)
Положения и скорости в интервале от a до
b вычисляются
по формулам
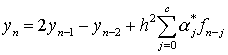 ,
, ![]() ,
,
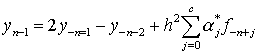 ,
, ![]() , (8.49)
, (8.49)
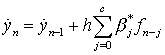 ,
, ![]() ,
,
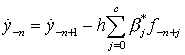 ,
, ![]() . (8.50)
. (8.50)
Совокупность формул (8.47) – (8.50) позволяет
вычислить начальную таблицу интегрирования. Обычно это делается путем
последовательных приближений.
Далее,
для вычисления ![]() и
и ![]() используются формулы
предсказания
используются формулы
предсказания
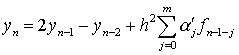 ,
,
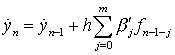
и коррекции
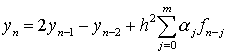 ,
,
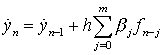 .
.
Величины параметров m и c подбираются эмпирическим путем исходя из особенностей
задачи.
8.6.
Сравнительная характеристика методов
Дадим
краткую сравнительную характеристику по точности и быстродействию представленных
здесь численных алгоритмов. Более подробное изложения результатов исследования
эффективности численных алгоритмов можно найти в книгах (Бордовицына, 1984) и
(Бордовицына и др., 1991).
Анализ
результатов многочисленных исследований по сопоставлению эффективности
представленных здесь численных методов в различных задачах динамики небесных
тел, как естественных, так и искусственных, позволяет сделать следующие выводы:
· при соответствующем выборе системы уравнений, порядка
метода, шага интегрирования и длины разрядной сетки ЭВМ высокой точности
вычисления орбит можно достичь любым из изложенных в настоящем разделе методов;
· однако с учетом быстродействия наиболее
эффективным практически во всех задачах
небесной механики следует считать метод Эверхарта, на втором месте окажутся
метод Булирша и Штера и метод Адамса-Мультона-Коулла, а на третьем алгоритмы
Рунге-Кутты-Фельберга.