9. Методы стабилизации и регуляризации уравнений движения.

9.1. Стабилизация уравнений орбитального движения

Как было отмечено в предыдущей главе, ляпуновская неустойчивость дифференциальных уравнений создает при численном интегрировании благоприятные условия для культивирования всевозможных ошибок, неизбежно сопровождающих любой численный процесс. Ошибки на текущем шаге интегрирования становятся ошибками начальных данных следующего, которые в дальнейшем усиливаются неустойчивостью шаг за шагом. Поэтому устойчивые уравнения для численного интегрирования более предпочтительны.

Задача стабилизации, о чем пойдет речь ниже, заключается как раз в том, чтобы ослабить влияние ляпуновской неустойчивости на численное решение и улучшить таким образом поведение неустранимых ошибок интегрирования.

Родоначальниками стабилизации в небесной механике бесспорно можно считать Дж. Баумгарта и П. Накози. Их стабилизирующие методы основаны на применении известных интегралов, которые содержат дополнительную информацию о решении и рассматриваются как необходимые условия, предъявляемые к решению.

Технически стабилизация достигается путем исправления численного (ошибочного) решения за его уклонение от интегральной поверхности в фазовом пространстве интегрируемых переменных. В возмущенной задаче, когда интегральная поверхность динамична, а ее интегральный параметр становится переменным, для оценки уклонений решения используются те же интегральные соотношения, однако система уравнений дополняется уравнением для интегрального параметра, которое интегрируется численно совместно со всей системой (Baumgarte, 1973; Бордовицына, Сухоплюева, 1980).

Стабилизация применяется как непосредственно к самому решению в процессе интегрирования (Накози, 1971), так и посредством введения дополнительных так называемых стабилизирующих членов в дифференциальные уравнения (Baumgarte, 1973). Очевидно, в этом случае стабилизация тем эффективнее, чем слабее возмущения и чем медленнее меняются параметры опорных интегральных поверхностей.

Из всех интегральных соотношений авторы стабилизирующих методов выделяют энергетические, поскольку, как показывает практика, именно стабилизация по энергии является наилучшим подспорьем в борьбе с ляпуновской неустойчивостью.

9.2. Неустойчивость кеплеровского движения

Рассмотрим две кеплеровские орбиты и , которые отличаются друг от друга в некоторый начальный момент времени на малые векторные величины и .

Из формул задачи двух тел нетрудно показать, что с точностью до малых первого порядка отклонение будут удовлетворять оценке

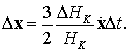(9.1)

Здесь — кеплеровская энергия, которая является интегралом орбиты (для определенности); — разность кеплеровских энергий, .

Если теперь одно из двух решений рассматривать как точное, скажем опорное , а другое, смежное , — как ошибочное, обусловленное ошибкой в начальный момент времени, то формулу (9.1) можно использовать как оценку ошибки ошибочного решения на любой другой момент времени.

Оценка (9.1) показывает, что эволюция носит периодически вековой характер: в целом ошибка растет по величине со временем , то локально увеличиваясь к перицентру, когда скорость и ускорение возрастают, то локально уменьшаясь к апоцентру, когда скорость и ускорение убывают. Также видно, что средняя скорость роста явно зависит от относительной ошибки в среднем движении: чем меньше , тем ниже скорость . Однако, какой бы малой ни была , всегда наступит такой момент времени, когда станет недопустимо большой. Собственно говоря, так обнаруживает себя ляпуновская неустойчивость.

Когда кеплеровская орбита интегрируется численно, ошибки подобные и возникают на каждом шаге интегрирования. Они, в свою очередь, отклоняют вычисляемую орбиту от интегральной поверхности, задаваемой энергией в фазовом пространстве координат и их производных. Это отклонение обнаруживает себя, главным образом, как линейный рост , но в соответствии с (9.1) это приводит к квадратичному росту .

Таким образом, для того чтобы ослабить влияние ляпуновской неустойчивости на точность численного решения, необходимо тем или иным способом в процессе интегрирования производить искусственную коррекцию вычисляемых переменных, которая бы укладывала ошибочное решение на интегральную поверхность и тем самым бы уменьшала . В этом и состоит задача стабилизации.

9.3. Метод Баумгарта

Простой, но мощный метод стабилизации был предложен Дж. Баумгартом (Baumgarte, 1973). Метод Баумгарта основан на идее искусственного введения в дифференциальные уравнения движения так называемых стабилизирующих (возмущающих) членов, компенсирующих отклонения численного (ошибочного) решения от некоторой опорной интегральной поверхности (точного решения). Практическое применение метода Баумгарта довольно широко и не ограничивается только задачами динамики. Рассмотрим метод на примере систем обыкновенных дифференциальных уравнений первого порядка.

Пусть система уравнений первого порядка

(9.2)

имеет интеграл

(9.3)

где — вектор интегрируемых переменных, — независимая переменная, — известная вектор функция и .

Будем стабилизировать систему (9.2) по опорной интегральной поверхности, задаваемой уравнением

(9.4)

причем для точного решения .

Следуя Баумгарту, систему (9.2) после введения стабилизирующих членов можно переписать в виде

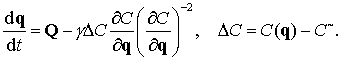(9.5)

Здесь — так называемый стабилизирующий параметр, который выбирается опытным путем.

Полученные уравнения (9.5) особенны тем, что они асимптотически устойчивы по , т.е. при для любых . Иначе говоря, при любых ошибках интегрирования дифференциального уравнения (9.5) его решение будет всегда стремиться “лечь” на интегральную поверхность (9.4).

Использование интегралов в качестве дополнительной информации о численном решении иногда позволяет существенно ослабить влияние ляпуновской неустойчивости на ошибки численного интегрирования. Однако в большинстве случаев применение интегральной стабилизации не эффективно, поскольку, очевидно, не все интегралы, даже если они имеются, хороши для стабилизации как средства борьбы с ляпуновской неустойчивостью и это обстоятельство значительно ограничивает область применения интегральной стабилизации.

Тем не менее, в небесной механике интегральная стабилизация надежно зарекомендовала себя как великолепное подспорье для решения многих прикладных задач.

Пусть теперь система уравнений (9.2) возмущается некоторой функцией

(9.6)

В возмущенном случае опорное значение интегральной функции становится переменной и, как нетрудно показать, ее поведение будет описываться дифференциальным уравнением

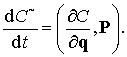(9.7)

Как и в невозмущенном случае, введем в систему (9.2) те же стабилизирующие члены, поскольку здесь они также будут удовлетворять условию асимптотической устойчивости по .

Так как для вычисления стабилизирующих членов используется переменная , стабилизация в этом случае предполагает включение уравнения (9.7) в возмущенную систему.

В результате стабилизированная система в возмущенном случае примет вид

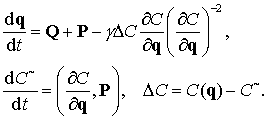(9.8)

С аналитической точки зрения, при стабилизированная система (9.8) эквивалентна системе (9.6), так как . Однако в отличие от последней первая асимптотически устойчива по . Это свойство дифференциальных уравнений весьма ценно при численном интегрировании, поскольку оно позволяет удерживать насаждаемое всевозможными ошибками численное решение около интегральной поверхности, учитывая при этом топологические свойства точного решения. Тогда как численное интегрирование нестабилизированных уравнений сопровождается дрейфом ошибки от интегральной поверхности.

Говоря о начальных условиях стабилизированной системы, следует заметить только, что стартовое значение переменной задается по начальным значениям переменных :

Несмотря на то, что после стабилизации уравнения становятся сложнее и требуют больше вычислительного времени, они могут значительно повысить оперативность интегрирования за счет своих замечательных свойств, так как стабилизация позволяет увеличить шаг интегрирования, сохраняя при этом точность численного решения.

9.4. Возмущенная задача двух тел

Рассмотрим стабилизацию Баумгарта на примере задачи двух тел, уравнения которой можно представить в виде

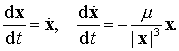(9.9)

Здесь m — гравитационный параметр.

В данном случае выберем энергию в качестве интеграла, по которому будем выполнять стабилизацию:

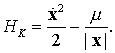(9.10)

Следуя Баумгарту, получим стабилизированную по энергии систему

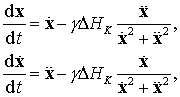(9.11)

где — отклонение энергии, вычисляемой по формуле (9.10), от опорной , а

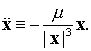
Хотя сам Баумгарт изначально получил другие стабилизированные уравнения, на наш взгляд, более эстетичного вида. В качестве исходных он взял уравнения задачи, записанные в виде системы уравнений второго порядка:

(9.12)

к которым и применил свою стабилизацию, разработанную им же для подобного рода систем. В итоге он получил следующие стабилизированные по энергии уравнения

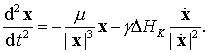(9.13)

В возмущенной задаче двух тел уравнения движения можно представить в виде

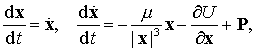(9.14)

где — потенциальная функция консервативных возмущающих сил, — неконсервативные силы, а в качестве интеграла примем полную энергию

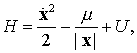(9.15)

которая является интегралом системы в консервативной задаче.

После стабилизации уравнения возмущенной задачи (9.14) преобразуются к виду

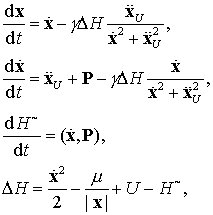(9.16)

где

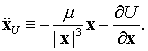
Так же, как и в невозмущенном случае, стабилизация применительно к системе уравнений второго порядка дает более эстетичные уравнения

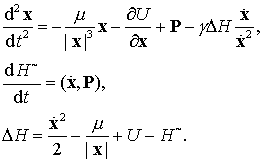(9.17)

Безусловно, утверждение о ляпуновской устойчивости стабилизированной системы (9.16) весьма сомнительно. Это, вообще говоря, нужно доказывать. Но, даже если после стабилизации система не становиться устойчивой, то, по крайней мере, можно полагать, что при слабых возмущениях "остаточная" неустойчивость будет мала в сравнении с устраняемой неустойчивостью. Очевидно, что эффективность применения стабилизированной системы будет тем выше, чем слабее будет влияние неконсервативных сил .

Говоря о численных аспектах в применении стабилизированных уравнений на практике, следует отметить следующее. В уравнения движения искусственно вводятся возмущающие (стабилизирующие) члены, которые не рассматриваются в физической постановке задачи. В связи с этим встает вопрос об адекватности решения системы (9.16) реальному орбитальному движению, описываемому системой (9.14).

С вычислительной точки зрения, строго говоря, ни одна из систем не описывает адекватно реальное движение, так как их численное интегрирование сопровождается численными ошибками. В этом случае уместно говорить о степени неадекватности систем, сравнивая их решения с точным аналитическим.

Как показывает практика, численное интегрирование стабилизированной системы (9.16) обеспечивает устойчивое (невозрастающее) поведение ошибки в энергии и линейное в координатах, тогда как интегрирование соответствующей неустойчивой системы (9.14) приводит к линейному росту ошибки в энергии и квадратичному (суперлинейному) в координатах. Эти результаты согласуются с оценками (9.1).

Следует заметить, что, поскольку стабилизация выполняется по энергии, то она обеспечивает сохранение только тех переменных, которые непосредственно связаны с энергией, таких как большая полуось, среднее движение, или орбитальный период. В то же время введение в уравнения движения стабилизирующих возмущающих сил влечет дополнительные численные ошибки в других орбитальных элементах, которые, однако, не приводят к вековым ошибкам в координатах и их производных. Поэтому стабилизирующие преобразования целесообразно применять лишь при интегрировании на длительных интервалах времени от нескольких десятков орбитальных периодов и более, где явно раскрывается практическая ценность стабилизации.

Использование стабилизированной системы остается эффективным даже в случае, когда опорная энергия стартует от значения, которое лишь приближенно соответствует истинной энергии в начальный момент времени, т.е. . Как было показано, постоянная ошибка приводит, главным образом, к линейному росту ошибки и поэтому несоответствие между начальными значениями задаваемой и истинной энергией существенно не изменит характер поведения численной ошибки . Но все же случай равенства остается наиболее предпочтительным. В связи с этой особенностью стабилизированной системы (9.16) опорную величину можно рассматривать как самостоятельную переменную, не зависящую от начальных условий, а в невозмущенном случае — как параметр.

В этом смысле известные уравнения в кеплеровских элементах также стабилизированы, если интегрируемые переменные, непосредственно связанные с энергией, рассматривать как самостоятельные. В невозмущенном движении такие переменные обращаются в постоянные параметры. Тогда вся система уравнений становится устойчивой по всем интегрируемым переменным за исключением энергетических. То же самое, например, можно сказать о системах теории Кустаанхеймо-Штифеля (Штифель, Шейфеле, 1975) или о системах уравнений Шперлинга-Боде (Silver, 1975).

9.5. Регуляризация уравнений движения. Преобразование Кустаанхеймо-Штифеля

Будем рассматривать движение материальной частицы с массой в поле тяготения центрального тела с массой под действием консервативны сил с потенциальной функцией и неконсервативных сил . Тогда дифференциальные уравнения движения частицы в прямоугольной системе координат, связанной с центральным телом , можно представить в виде

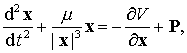(9.18)

с начальными условиями

(9.19)

где — вектор положения, — физическое время, , — универсальная гравитационная постоянная, .

Уравнения (9.18) сингулярны в окрестности начала координат. Для орбит, имеющих большие эксцентриситеты, наличие особенности в начале координат приводит к сильным и неравномерным изменениям функций правых частей уравнений движения. При численном интегрировании такая неравномерность требует постоянного изменения шага интегрирования. Это снижает точность численного интегрирования и приводит к непроизводительным затратам машинного времени.

Регуляризировать уравнения движения и их решения позволяет преобразование Кустаанхеймо-Штифеля (KS) вместе с временным преобразованием Сундмана (Штифель, Шейфеле, 1975), осуществляющим переход к новой независимой переменной , называемой фиктивным временем. Регуляризирующее преобразование Кустаанхеймо-Штифеля задает отображение физического пространства () в четырехмерное KS-пространство () и представляется в виде

(9.20)

где

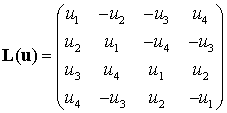(9.21)

— матрица KS-преобразования, — 4-мерный вектор положения в KS-пространстве. Причем для и справедливо соотношение

Необходимо заметить, что в (9.20) вектор дополняется нулевой четвертой компонентой: .

В результате уравнения движения в новых переменных преобразуются к виду

(9.22)

Подставляя в (9.22) энергетическое соотношение

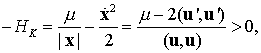
получим уравнения возмущенного гармонического осциллятора

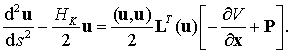(9.23)

Система (9.23) не замкнута и ее следует дополнить дифференциальными уравнениями для энергии и времени

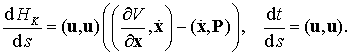(9.24)

При исследовании возмущенного эллиптического движения удобнее в качестве независимой переменной рассматривать так называемую обобщенную эксцентрическую аномалию .

Предполагая, что полная энергия

переменную введем с помощью дифференциального соотношения

(9.25)

где — частота системы. Замена независимой переменной приводит к новой системе дифференциальных уравнений

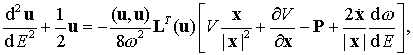(9.26)

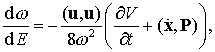(9.27)

(9.28)

Полученные таким образом уравнения и их решения полностью регулярны в окрестности соударения с центральным телом. При отсутствии возмущений решение в KS-пространстве представимо в форме

,

где регулярные оскулирующие элементы — векторные константы.

Скорость изменения функций правых частей в уравнениях (9.26), (9.28) можно понизить, перейдя с помощью известного метода вариации произвольных постоянных к уравнениям в регулярных элементах . Принимая обозначение , систему дифференциальных уравнений в регулярных элементах можно записать в виде

(9.29)

(9.30)

с начальными условиями

(9.31)

где

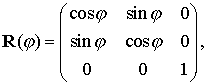(9.32)

— вектор возмущений, компоненты которого — четырехмерные вектора, а — скаляр:

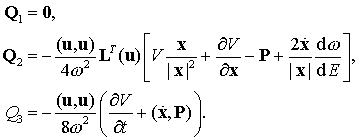(9.33)

Точность численного интегрирования уравнения для быстрой переменной (9.30) чувствительна к значению эксцентриситета, поскольку величина как функция даже в невозмущенном движении может меняться сложным образом. Поэтому целесообразно использовать временной элемент , который изменяется почти линейно в слабовозмущенном движении и связан с физическим временем соотношением

Дифференцируя правую и левую части этого соотношения и разрешая его относительно производной , получим дифференциальное уравнение

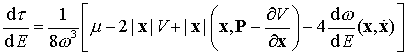(9.34)

с начальным условием

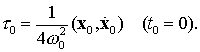(9.35)

Численные эксперименты показывают, что в случае возмущенного эллиптического движения алгоритм с дифференциальным уравнением для временного элемента лучше по точности вычисления времени, чем алгоритм с дифференциальным уравнением времени.

Таким образом, система (9.29), (9.34) становится полностью нечувствительна к изменению эксцентриситета. Однако она по-прежнему содержит уравнение для быстрой переменной, которое будет определять размер шага интегрирования.

Кроме того, очевидно, что при численном интегрировании на ЭВМ с ограниченной разрядной сеткой текущие вычисления неограниченно возрастающих величин типа за счет округления (усечения) производят неограниченно возрастающие ошибки, которые могут усиливаться ляпуновской неустойчивостью.

Кроме того, самостоятельной проблемой для всех перечисленных здесь вариантов регуляризированных уравнений является проблема точного выхода в физическое пространство на заданный момент физического времени.

9.6. Преобразования, исключающие дифференциальное уравнение для быстрой переменной из системы уравнений движения. Метод Шарковского.

Попытка решить проблему точного выхода в физическое пространство на заданный момент физического времени и одновременно устранить уравнение для быстрой переменной из интегрируемой системы была предпринята Н.А. Шарковским (1998).

Подход Шарковского основан на использовании в качестве независимой переменной невозмущенной эксцентрической аномалии и применении свойств матриц поворота (9.32). (Здесь и ниже индекс обозначает переменные в кеплеровском движении.)

Переход к новой независимой переменной осуществляется с помощью преобразования

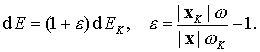(9.36)

Тогда уравнения (9.29), (9.30) преобразуются к виду

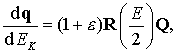(9.37)

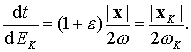(9.38)

Уравнение (9.38) интегрируется в квадратурах

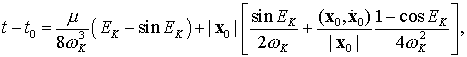(9.39)

что позволяет исключить его из системы дифференциальных уравнений, решаемой численно, или, иначе говоря, понизить порядок системы. Правые части уравнений (9.37) еще зависят от . Чтобы привести их к зависимости от новой переменной , воспользуемся основными свойствами ортогональных матриц , согласно которым для любых вещественных значений и

Применяя эти свойства к уравнениям (9.37) и предполагая, что ( — отклонение возмущенной эксцентрической аномалии от невозмущенной), приведем их к виду

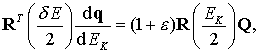
(9.40)

Преобразуем левые части уравнений (9.40)

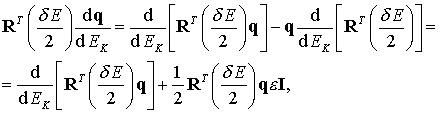
где

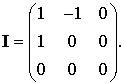
Обозначая через , получим следующую окончательную систему

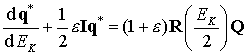(9.41)

c начальными условиями (9.31).

Алгоритм Шарковского был апробирован в задачах динамики близких спутников планет (Шарковский, 1998) и зарекомендовал себя как высокоэффективный по точности вычислений и быстродействию.

Далее